

And, so is ∠ADC, and we have our second pair of congruent angles. By definition, that means that the angle it creates with the base (∠ADB) is a right angle. So here, we know that AD is the height to the base.
#HEIGHT OF ISOSCELES TRIANGLE HOW TO#
So we will find or construct another pair of congruent angles or another pair of equal sides, and use one of the triangle congruency postulates to show the two triangles are congruent. In this video, I teach you how to find the height, length of each side, perimeter, and area of an isosceles triangle from a word problem. The altitude of the triangle is four - thirds the altitude of the segment. What is the value of P (which is an angle) P may be an angle but you have not told us which one. The area of isosceles triangle ½ × Base × Height The perimeter of isosceles triangle sum of its three sides written as, P 2a + b The altitude of isosceles triangle h (a2 b2/4) You can also find the area of the isosceles triangle using the following formulas: A ½ (a2 b2 4) × b with all three sides. Find the minimum isosceles triangle circumscribed about a parabolic segment. We already have a pair of equal edges (the legs, per the definition of an isosceles triangle) and a pair of congruent angles (per the Base Angles Theorem). The height of the isosceles triangle is 30cm and the base 20cm. The strategy for this and for the remaining similar problems (showing that the altitude to the base bisects the apex angle, showing that the angle bisector is perpendicular to the base, etc.) will be the same. How to Calculate the Angles of an Isosceles Triangle.
#HEIGHT OF ISOSCELES TRIANGLE PLUS#
Prove that in isosceles triangle ΔABC, the height to the base, AD, bisects the base. The leg length a is equal to the square root the height h squared plus the base b divided by 2, squared.
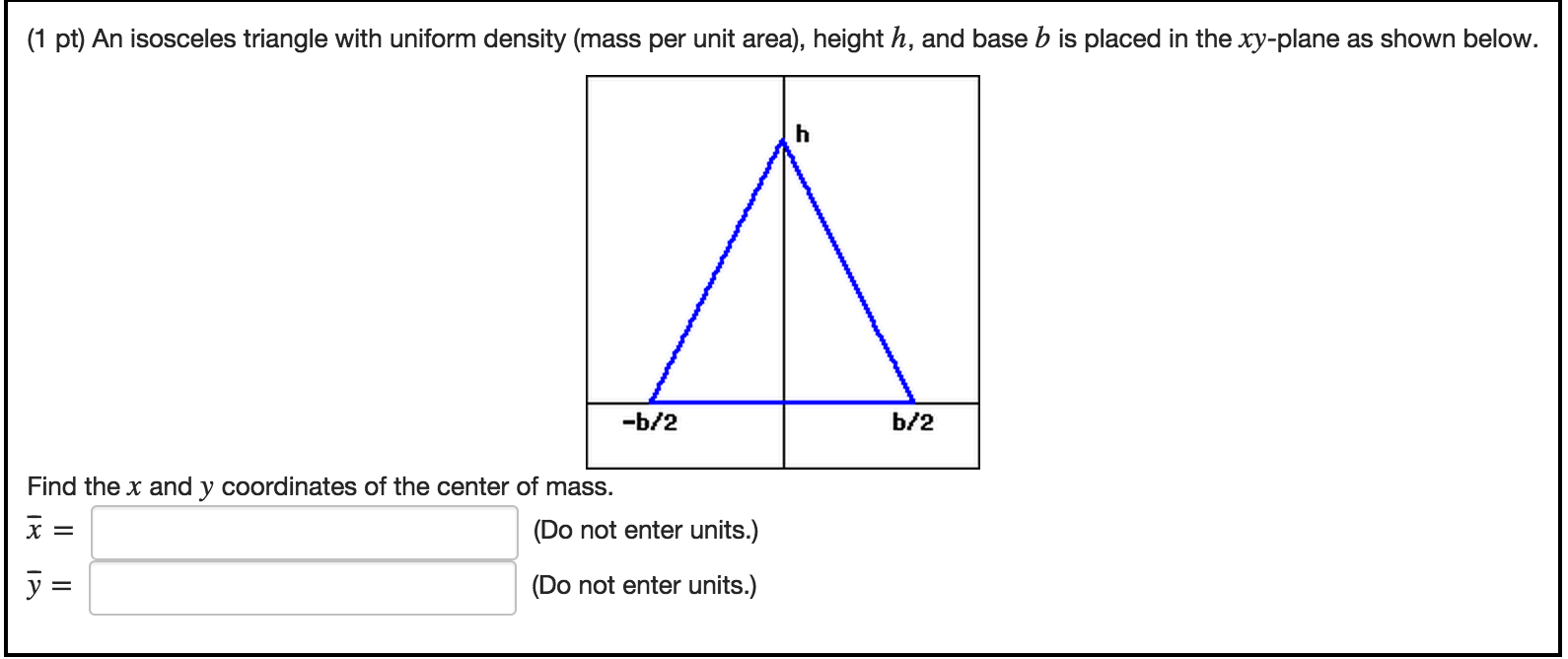
Let's start by proving that in an isosceles triangle, the height (or altitude) to the base bisects the base. In an isosceles triangle, the height drawn to the base is both the median and the angle bisector. With these two facts in hand, it will be easy to show several other properties of isosceles triangles using the same method (triangle congruency). Having proven the Base Angles Theorem for isosceles triangles using triangle congruency, we know that in an isosceles triangle the legs are equal and the base angles are congruent. I have added an attachment that represents the given trapezoid. In this video, I teach you how to find the height, length of each side, perimeter, and area of an isosceles triangle from a word problem. Because the trapezoid is isosceles, the 2 legs of the trapezoid will be equal. The common length of these lines is the height of the triangle. An isosceles trapezoid has 2 parallel sides and equal non-parallel legs.The height of the isosceles trapezoid is 2.65 m. In today's lesson we'll learn a simple strategy for proving that in an isosceles triangle, the height to the base bisects the base. In an isosceles triangle, angle bisector, median and altitude from apex to the base coincide.


 0 kommentar(er)
0 kommentar(er)
